モールス符号から考える符号化理論

こんにちは。M1のYukimuraです。
最近モールス符号の勉強をしているのですが、ちょっと難しいなと感じたことがあったので、そのことを符号化理論の観点から話したいと思います。

モールス符号とは

モールス符号とは、「・」(トン,短点)と「ー」(ツー,長点)の２つの符号を用いて文字や記号を符号化する、可変長符号化手法で、主に電信符号として用いられることが多いものです。
有名どころだと「・・・_ーーー_・・・」で「SOS」、「ー・ー・_ーー・ー_ー・・」で「CQD」なんて言うのがあります。(読みやすさの都合上、スペースの代わりに_を入れています)
またジブリ映画でも「天空の城ラピュタ」の飛行戦艦ゴリアテからの暗号無線をドーラが傍聴するシーンや、「崖の上のポニョ」でそうすけとリサと耕一がモースル符号を使って信号灯で会話しているシーンは、記憶に残っている方がいるかも知れません。

さて、日本で使われるものは、欧文モールスと和文モールスの２つがありますが、今回は特に(今私が勉強している)欧文モールスについて考察・検討します。符号語(トンツー)とアルファベット・数字の一覧を以下に示します。

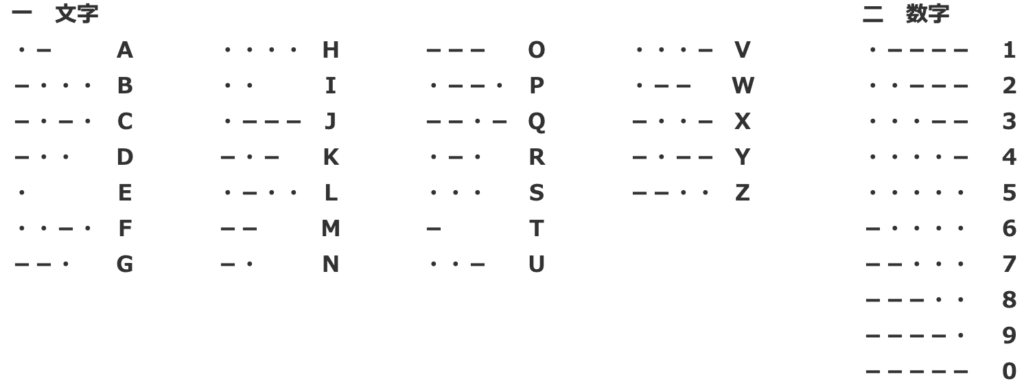
ちなみに欧文モールスでは、使用頻度の高い文字が短い符号語で表されるように設計されています(E,Tなどは使用頻度が高く、J,Yなどは低い)。こういうものをエントロピー符号といいますが、実に合理的です。(さらにちなみに、和文モールスは、いろは順に欧文モールスを当てはめただけなので、エントロピー符号ではありません)

モールス符号の問題点

さて、モールス符号を勉強をしていると気づくのですが、モールス符号は接頭符号(Prefix code)ではないことがわかります。
「接頭符号ではない」、というのは「全ての符号が必ずしも頭語属性を満たさない」ということであり、「頭語属性を満たさない」とは、「ある符号語が他の符号語の接頭部になっている」ということです。
もっとわかりやすく言えば、{「パン」「パンツ」「パンジャンドラム」「パンアメリカン航空」「アメリカン航空」}という5つの符号語がある符号は「接頭符号ではない」といえるということです。(これをここでは仮に「パン符号」と呼びます)

これがどういうことで何が困るか、というと、パン符号で「パン」が送信されたときに、受信者としては「パン...」と聞いた時点で、次の文字を聞くまで「パン」であることを確定できないことに問題があります。また、「パンアメリカン航空」と送信されたときに、「パン」「アメリカン航空」と理解される可能性も否めません。

この問題を解決するためには、パン符号を、符号語を接頭部に含まない形にする必要があります。具体的には、{「食パン」「パンツ」「パンジャンドラム」「パンナム航空」「アメリカン航空」}という形に変形すると良いでしょう。

さて話をモールス符号に戻すと、見ての通り接頭符号ではありません。
例えばA(・ー)はJ(・ーーー)やL(・－・・)の接頭部ですし、I(・・)はF(・・－・)やH(・・・・)の接頭部です。モールス符号では一般に、全部聞き終わらないうちにある程度どの符号語かを理解しないと、全文を聞き取れないのですが、こんな調子では到底聞き取れません。さらに、区切りがわかりにくい高速でのモールス通信ではさらに悲惨で、「・ー ー・」と来たときに、「AN」なのか「P」なのかがわかりません。私が勉強不足な面が多分にあるのですが、どうも設計上の問題じゃないか、というような気もします。つまり接頭符号であれば、こんな苦しみは無いのではないか、と。

しかし、こちらは先程と事情が違い、「食」をつけたり少し変形したりしてどうにかするわけにはいきません。

ハフマン符号

ここで着目したのがハフマン符号です。ハフマン符号とは、エントロピー符号であって接頭符号である符号化手法の中で、平均符号長が最短となる符号です。
既存のモールス信号では先述の通り接頭符号では無いため諸々不便が生じますが、ハフマン符号を使うことで接頭符号を設計でき、かつその中でも最短なものを作ることができます。

1848年にFriedrich Clemens Gerkeによって原案が考案されたモールス符号に対して、1952年に考案されたハフマン符号を持ち出して争うことは、些か不公平な気もしますが、実験的に符号化してみましょう。

ハフマン符号は以下のようにして作成します

1. 出現頻度の大きさの順にアルファベットを並べる。
2. 頻度の小さい2つのアルファベット(葉)を選び、２本の枝で合流させ、合流点に2つの頻度の和を割り当てる。
3. 合流点を1つの節点とみなし、2.と同様に、頻度の小さい2つの葉もしくは節点を選び、２本の枝で合流させ、合流点に2つの頻度の和を割り当てる。
4. 以上の 1.,2.,3.を、合流がなくなるまで繰り返す。
5. 右端のから左方へ枝のビットを辿り、それを符号語として左先端のアルファベットに割り当てる。

以降の計算について、アルファベットの出現頻度は下図の通り、GoogleCorpusDataを用いた研究を用いることとします。

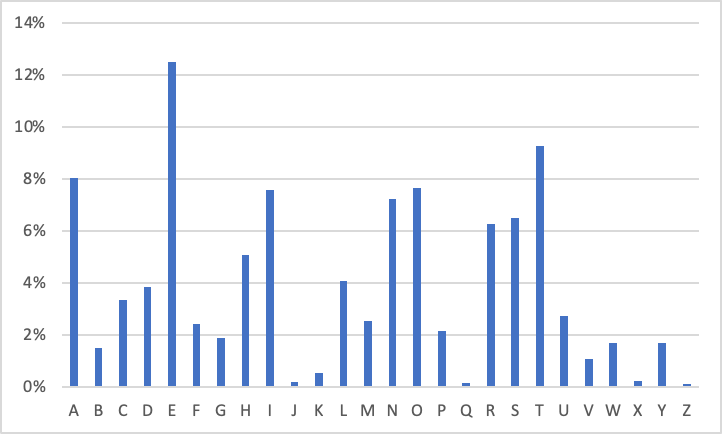
上グラフの出現頻度を用いてハフマン符号を作成した結果が以下です。

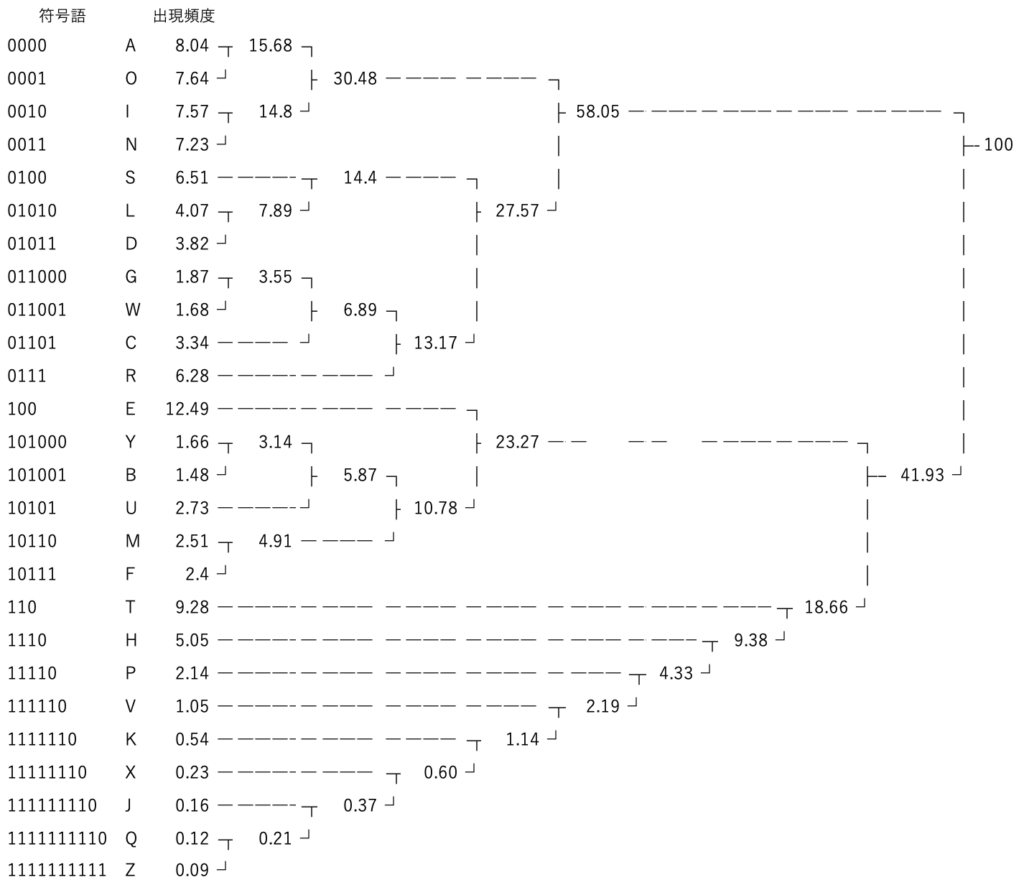
下の方、10桁とだいぶ桁数が大きくなってしまいましたね。また一番小さくても桁数が3と、従来のモールス符号より大きくなっています。

01ではわかりにくいため、上図一番左側のビット列について、0を短点、1を長点として扱うと、以下のようになります。

おー！！！！、一気に電信符号っぽくなりました！！！！
今回作った符号、以降の説明の簡単のために「ゆ式電信符号」と名付けました。

これでどんなに符号語の間隔が短くても、最初からきちんと聞けていれば一意に復号可能です。

しかし、作ってみてからわかったことなのですが、QやZなどが長くなりすぎて、実用には適さないような気がします。また、Qが長くなってしまってから気づいたのですが、Qという文字は全局呼び出しである「CQ」でよく使うので、本来は英単語での出現頻度表ではなく、無線電信における出現頻度表を使うべきであったと思いました。

さて、「使いにくそう」では漠然としているので、実際に数値で見てみます。もしかしたら数値的には「ゆ式電信符号」のほうが優れているかも知れません。
欧文モールス符号と「ゆ式電信符号」について、実際に電信として打ったときの平均長(平均時間長)を計算します。ただし無線局運用規則（昭和二十五年電波監理委員会規則第十七号）の別表に「一線の長さは、三点に等しい。」と定めがあるため、長点は短点3点分の時間がかかるものとします。また併せて、符号語の文字列的な長さから平均符号長も算出し比較してみます。

	平均時間長	平均符号長
欧文モールス符号	4.5268	2.5284
ゆ式電信符号	8.0848	4.1924

...はい。平均時間長、平均符号長とも2倍近くなってしまいました。

ということで、今回開発された「ゆ式電信符号」は、接頭符号であるため、符号語と符号語の間が明瞭でなくとも一意に復号できる一方、従来の欧文モールスの倍近い時間がかかるものになってしまいました。みなさんなら、「聞き取りやすいが長い」ゆ式電信符号と、「短いが聞き取りにくい場合がある」欧文モールス符号、どちらを使いたいですか？

おわりに

モールス符号が覚えられないという単純な悩みから端を発した今回の記事でした。

先日、穐山先生から「一回生向けの記事を書いてみては？」というアドバイスを頂いたので、一回生配当科目「情報理論」で学ぶ内容を前提に執筆しました。情報理工学部の1回生は、春セメスター金曜3限の内容を思い出しながら読んでくれていたら嬉しいです。

しかしまあ、150年以上前に作られた符号ながら、モールス信号というのはよくできているなと感じます。普及度×符号としての利便性で他に代わるものがないから150年も地位を保ち続けているわけで、改めて感心するものでした。
覚えて損はないものなので、皆様も是非、一緒にモールス符号の勉強をしてみませんか？？？

(文責:2022年度M1 木村 悠生)